When will human civilization end?
I don’t know the precise answer to that question (no one does), but here I’d like to share with you one way of trying to answer it. The results are not good.
Introduction
This post is a mostly non-technical summary of a mathematically encrusted article published online last week in the International Journal of Astrobiology. The article is copyright-free, so please feel free to download, share, and re-post it from here: “Biotechnology and the Lifetime of Technical Civilizations.”
Everyone has a stake in the topic! If you hunger for more detail, more context, more rigor, or the usual academic hedging, please consult the paper. (In all seriousness, the results below depend on many assumptions, so please consult the paper for a full enumeration.)
tl;dr
Today, only two people could destroy civilization on earth: the leaders of Russia and the United States, who each control enough nuclear weapons to do the job. If the number of potential civilization-destroyers stays at two, and if each has less than a 0.035% chance per year that they will pull the civilization-ending trigger, then a simple math formula (equation A3 in the paper) shows that earth’s civilization has a 50% chance of surviving for 1000 years.
So far, so good (sort of).
But what happens when a civilization-ending technology gets into many more hands? It seems obvious that destruction risk increases with the number of hands. But how much?
This is a pressing question because biotechnology could soon become a civilization-ending technology. The equations in the paper apply to any technology that could end civilization, but biotechnology is a special concern because natural biology, in the form of great plagues, has ended local civilizations on earth. (Example: the Aztecs and smallpox.) The exponential advancements in human-made biotechnology – a field that did not even exist 50 years ago – could, in the not-distant future, enable many persons in many hospitals to engineer microbes specially designed to kill cancer cells … or kill people.
So let’s imagine that 180,000 people on earth are able to use biotechnology to create a civilization-ending plague (that number is explained below), and let’s imagine that each one of them has only a one-in-a-million chance per year of pulling the trigger. Using the same math equation as above, that would give us a 50% chance of surviving to 4 years. That is not a typo – four years.
Yikes.
Please note: I am not saying the world will end in 4 years. Biotechnology has not yet developed to the point where 180,000 people wield the skills to erase civilization, and there is no guarantee it ever will. But, smart money would bet that, if nature can create plague organisms through the dumb chance of evolution, then clever humans can not only do it, too, but do it faster and “better” … once they have suitable tools.
That is the gist of the paper. Its intended message is: We should start now to plan for an era when the genie of destruction is widely out of the bottle. We don’t know when or if that era will arrive, but no one can guarantee it will not. The only guarantee is that being unprepared will be a nightmare. There is much more we could be doing.
The rest of this post explains some other elements of the paper:
- How to make your own estimates of civilizational lifespan.
- Where the number 180,000 came from (it wasn’t drawn from a hat).
- The universe’s apparent lifelessness is a bad sign.
Estimating Civilizational Lifespan Yourself
You may have different ideas about the number of people who can end civilization and how likely they are to do it. That’s great. Here’s how to use the paper’s mathematical model to estimate how long civilization will live.
-
Start with the number of people you believe can end civilization – call it E.
-
Next, assign the probability per year that each one of the people will pull the trigger to end civilization – call it P.
-
Then use equation A3 from the paper to compute: median lifespan = 0.7 ÷ (E × P).
“Median lifespan” means that a civilization has a 50% chance of lasting that long.
Or, use the graph below. Start on the X-axis at your value of E, trace vertically until you hit the line corresponding to your P value, and then ricochet horizontally to the Y-axis where you can read off the median lifespan. Note that both axes have logarithmic scales.
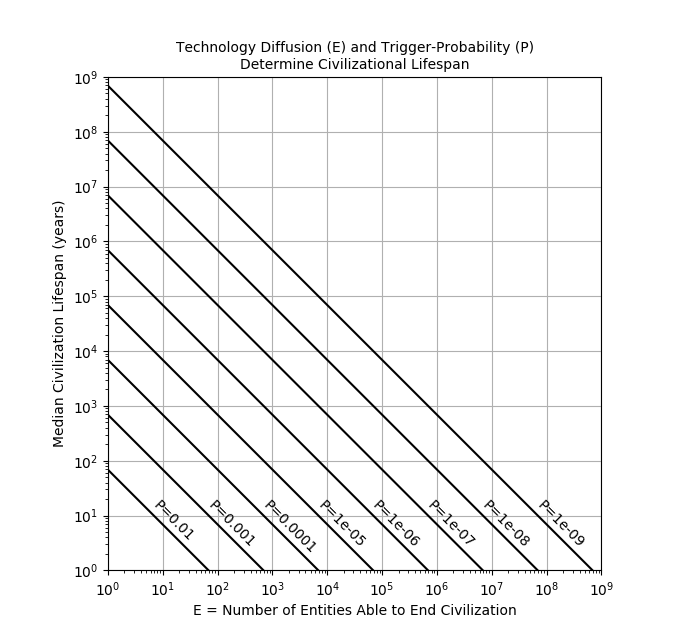 |
So, for example, if E=7000 and P=one-in-a-million (ten to the minus 6 power, or “1e-06”) then the median lifespan is 100 years (ten to the two power).
To calculate a lifespan that the civilization has a 95% chance of reaching, divide the median lifespan by 13.5.
180,000 Biotechnologists
For now, at least, it takes skill to use biotechnology. How many skilled biotechnologists are on earth today?
Here, too, there is no easy answer, but we can get a feel for the size of the talent pool by looking at the number of people who publish scientific articles about the topic.
Assuming that genetic tools will be the most dangerous aspect of biotechnology, a search of the PubMed database shows that about 1.5 million different people across the world published a scientific article about “genetic techniques” from 2008 through 2015.
But being a co-author on just one such paper is not of great significance. As an example, students who work for a summer in a laboratory can easily end up as a co-author even though most of their time was spent washing test tubes.
By the time an author’s name appears on five articles, however, it’s a different story. There is nothing magic about the number five, except that it indicates a rather substantial commitment and immersion in the field.
This is the source of the 180,000. Out of the 1.5 million authors, that is the number of scientists who wrote five or more articles and who, therefore, would be predicted to have reasonable skill at the lab bench.
The number will certainly grow as the technology matures and becomes more useful. There were not many computer programmers in 1969, but there are millions now.
A Lifeless Universe Is a Bad Sign: The Fermi Paradox
Before discussing more of the paper’s mathematical models in this section, it’s necessary to first set some context, beginning with the fact that scientists have been searching for signs of life in space since 1960, without success.
That’s surprising because the universe seems quite hospitable to life. Recent estimates say that 1,000,000,000,000,000,000,000,000 stars (that’s 24 zeros – one million billion billion) populate the universe, and that most will have planets, and that water is common on many types of worlds, if our solar system is a guide.
The universe has also allowed plenty of time – up to 13 billion years – for any early green-slime life-forms on these worlds to evolve into intelligent organisms with civilizations capable, like us, of communicating across interstellar distances.
Yet, except for humans, the universe appears devoid of intelligence, a constrast so stark that it has a name: “Fermi’s paradox.”
In a wonderfully accessible book, astronomer Stephen Webb reviews 75 theories proposed to explain the Fermi paradox. He frequently emphasizes, correctly, that it’s a tall order to find one explanation for the absence of detectable technical civilizations in the universe. Consider: if every one of the universe’s 1,000,000,000,000,000,000,000,000 star systems had a technical civilization, and if that one explanation failed in just 0.1% of cases, then the number of surviving technical civilizations would be a 1 followed by 21 zeroes – still a gigantic number (a billion trillion).
Returning to the paper’s models, it makes sense to ask if the predicted lifetime of technical civilizations could be a factor in Fermi’s paradox because, as explained in note 1, below, biotechnology is likely to be an inevitable development in advanced civilizations.
To start, let’s be very generous with our hypothesized E and P by assuming that only 10 people in a civilization have access to civilization-ending biotechnology, and that each has only one chance in a million annually of pulling the trigger. Equation A3 in the paper predicts a median lifespan of 70,000 years in this situation, meaning that, given a large number of such civilizations, half would be expected to survive 70,000 years.
That’s the happiest number we’ve seen yet!
But median lifespan is not the whole story. The paper’s model happens to tell us that, no matter what the median lifespan is, after just 80 times that duration, only one civilization in 1,000,000,000,000,000,000,000,000 (that’s 24 zeroes again) will still be alive.
That is a remarkable result. It predicts that, if every star in the universe had a technical civilization like the example above, at the time our earliest ancestors were first starting to walk upright 5.6 million years ago, then only one civilization would have survived until now. Five million years is an eye-blink in the universe’s history, just 0.04% of its age. In other words, even if advanced civilizations are common in space, they may be rare in time.
The graph below shows the survival of civilizations for other E and P, assuming we start with a civilization in every star system. It plots the number of surviving civilizations over time for 29 different combinations of E and P. It turns out that this reduces to just 7 different survival curves, depending on the value of E multiplied by P. When the survival curve hits the x-axis, only one civilization is left. The rightmost curve hits the x-axis at 5.6 million years.
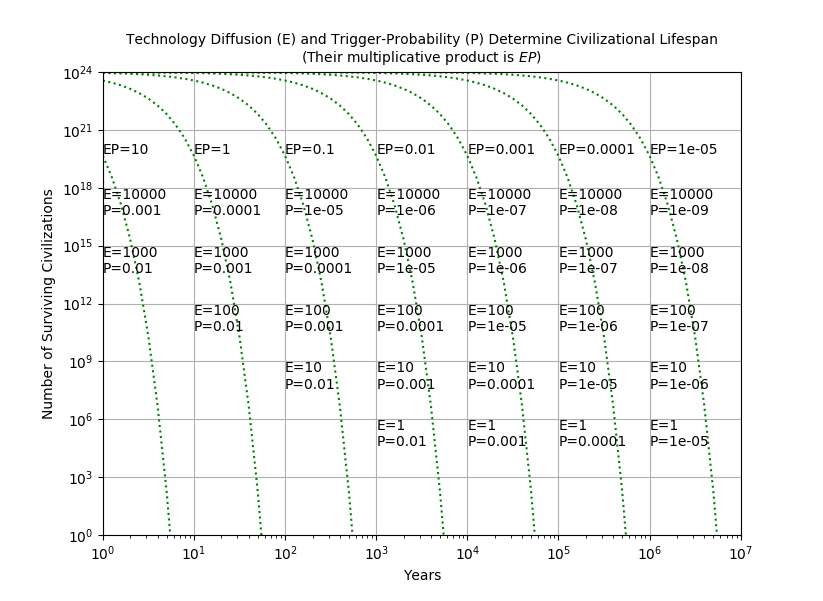 |
It is hard to find in the graph any good news for the long-term survival of advanced civilizations in the universe. As a shorthand, if a civilization has a given E and P, a universe of such civilizations is empty in 56÷(E×P) years.
Still, it is important to make a few comments.
-
The paper describes several assumptions behind its mathematical models. The longer the models are applied, the less likely the assumptions will hold. It is not clear, however, whether diverging from the assumptions will shorten or lessen the predicted lifespans. For example, figure 4 in the paper shows that a growth in E of just 1% per year can shorten civilizational lifespans even more.
-
It may be hoped that colonization of other planets could outpace the rate of civilizational deaths. This is unlikely. Mathematically, the only way to outpace the model’s civilizational death rate is to colonize at an exponential rate (because the decline in civilization numbers is exponential). We can be reasonably sure that exponential colonization has not occurred in our galaxy because, if it had occurred over long periods of time, the galaxy would be filled-to-bursting with advanced civilizations, and we just don’t see that. A steady-state balance between exponential dying and exponential colonizing could occur, but it would be a delicate affair.
What Does It All Mean?
The paper shows that, once a civilization-ending technology exists, the continued survival of civilization is merely a numbers game. What to do?
That question has bedeviled the human race since the 1940s, when some of its members first realized we had the capacity to erase what millennia of progress have so painfully built. In all cases of existential threat, whether it is nuclear weapons, or asteroid impact, or climate change, or super-volcanism, or plagues, effective response must be built on a foundation of understanding. Continued exploration of such threats, with wide discussion to make them less abstract, is, therefore, the beginning. The emptiness of the universe suggests that successfully mitigating them is very hard … and that we better get to work.
Notes:
[1] Reasoning for the universality of biotechnology starts with the safe assumptions that all life forms are subject to disease and that all intelligent life will, as a result of evolution, have self-preservation drives at the individual or group level. This means that intelligence leads to a desire for medicines, and desire for medicines leads to technology that manipulates the fundamental genetic processes that define life, i.e. biotechnology. [Return to text]