When will human civilization end?

I don’t know the precise answer to that question (no one does), but here I’d like to share with you one way of trying to answer it. The results are not good.

Introduction

This post is a mostly non-technical summary of a mathematically encrusted article published online last week in the International Journal of Astrobiology. The article is copyright-free, so please feel free to download, share, and re-post it from here: “Biotechnology and the Lifetime of Technical Civilizations.”

Everyone has a stake in the topic! If you hunger for more detail, more context, more rigor, or the usual academic hedging, please consult the paper. (In all seriousness, the results below depend on many assumptions, so please consult the paper for a full enumeration.)

tl;dr

Today, only two people could destroy civilization on earth: the leaders of Russia and the United States, who each control enough nuclear weapons to do the job. If the number of potential civilization-destroyers stays at two, and if each has less than a 0.035% chance per year that they will pull the civilization-ending trigger, then a simple math formula (equation A3 in the paper) shows that earth’s civilization has a 50% chance of surviving for 1000 years.

So far, so good (sort of).

But what happens when a civilization-ending technology gets into many more hands? It seems obvious that destruction risk increases with the number of hands. But how much?

This is a pressing question because biotechnology could soon become a civilization-ending technology. The equations in the paper apply to any technology that could end civilization, but biotechnology is a special concern because natural biology, in the form of great plagues, has ended local civilizations on earth. (Example: the Aztecs and smallpox.) The exponential advancements in human-made biotechnology – a field that did not even exist 50 years ago – could, in the not-distant future, enable many persons in many hospitals to engineer microbes specially designed to kill cancer cells … or kill people.

So let’s imagine that 180,000 people on earth are able to use biotechnology to create a civilization-ending plague (that number is explained below), and let’s imagine that each one of them has only a one-in-a-million chance per year of pulling the trigger. Using the same math equation as above, that would give us a 50% chance of surviving to 4 years. That is not a typo – four years.

Yikes.

Please note: I am not saying the world will end in 4 years. Biotechnology has not yet developed to the point where 180,000 people wield the skills to erase civilization, and there is no guarantee it ever will. But, smart money would bet that, if nature can create plague organisms through the dumb chance of evolution, then clever humans can not only do it, too, but do it faster and “better” … once they have suitable tools.

That is the gist of the paper. Its intended message is: We should start now to plan for an era when the genie of destruction is widely out of the bottle. We don’t know when or if that era will arrive, but no one can guarantee it will not. The only guarantee is that being unprepared will be a nightmare. There is much more we could be doing.

The rest of this post explains some other elements of the paper:

• How to make your own estimates of civilizational lifespan.
• Where the number 180,000 came from (it wasn’t drawn from a hat).
• The universe’s apparent lifelessness is a bad sign.

Estimating Civilizational Lifespan Yourself

You may have different ideas about the number of people who can end civilization and how likely they are to do it. That’s great. Here’s how to use the paper’s mathematical model to estimate how long civilization will live.

• Start with the number of people you believe can end civilization – call it E.

• Next, assign the probability per year that each one of the people will pull the trigger to end civilization – call it P.

• Then use equation A3 from the paper to compute: median lifespan = 0.7 ÷ (E × P).

“Median lifespan” means that a civilization has a 50% chance of lasting that long.

Or, use the graph below. Start on the X-axis at your value of E, trace vertically until you hit the line corresponding to your P value, and then ricochet horizontally to the Y-axis where you can read off the median lifespan. Note that both axes have logarithmic scales.

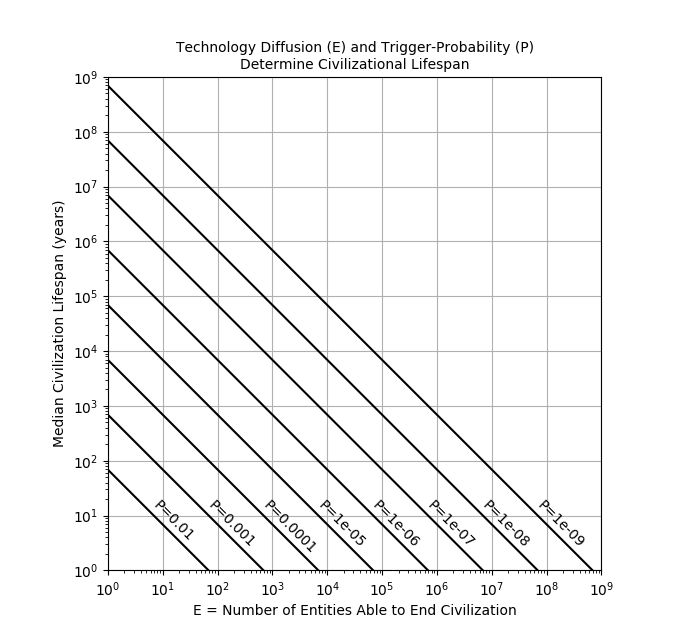So, for example, if E=7000 and P=one-in-a-million (ten to the minus 6 power, or “1e-06”) then the median lifespan is 100 years (ten to the two power).

To calculate a lifespan that the civilization has a 95% chance of reaching, divide the median lifespan by 13.5.

180,000 Biotechnologists

For now, at least, it takes skill to use biotechnology. How many skilled biotechnologists are on earth today?

Here, too, there is no easy answer, but we can get a feel for the size of the talent pool by looking at the number of people who publish scientific articles about the topic.

Assuming that genetic tools will be the most dangerous aspect of biotechnology, a search of the PubMed database shows that about 1.5 million different people across the world published a scientific article about “genetic techniques” from 2008 through 2015.

But being a co-author on just one such paper is not of great significance. As an example, students who work for a summer in a laboratory can easily end up as a co-author even though most of their time was spent washing test tubes.

By the time an author’s name appears on five articles, however, it’s a different story. There is nothing magic about the number five, except that it indicates a rather substantial commitment and immersion in the field.

This is the source of the 180,000. Out of the 1.5 million authors, that is the number of scientists who wrote five or more articles and who, therefore, would be predicted to have reasonable skill at the lab bench.

The number will certainly grow as the technology matures and becomes more useful. There were not many computer programmers in 1969, but there are millions now.

A Lifeless Universe Is a Bad Sign: The Fermi Paradox

Before discussing more of the paper’s mathematical models in this section, it’s necessary to first set some context, beginning with the fact that scientists have been searching for signs of life in space since 1960, without success.

That’s surprising because the universe seems quite hospitable to life. Recent estimates say that 1,000,000,000,000,000,000,000,000 stars (that’s 24 zeros – one million billion billion) populate the universe, and that most will have planets, and that water is common on many types of worlds, if our solar system is a guide.

The universe has also allowed plenty of time – up to 13 billion years – for any early green-slime life-forms on these worlds to evolve into intelligent organisms with civilizations capable, like us, of communicating across interstellar distances.

Yet, except for humans, the universe appears devoid of intelligence, a constrast so stark that it has a name: “Fermi’s paradox.”

In a wonderfully accessible book, astronomer Stephen Webb reviews 75 theories proposed to explain the Fermi paradox. He frequently emphasizes, correctly, that it’s a tall order to find one explanation for the absence of detectable technical civilizations in the universe. Consider: if every one of the universe’s 1,000,000,000,000,000,000,000,000 star systems had a technical civilization, and if that one explanation failed in just 0.1% of cases, then the number of surviving technical civilizations would be a 1 followed by 21 zeroes – still a gigantic number (a billion trillion).

Returning to the paper’s models, it makes sense to ask if the predicted lifetime of technical civilizations could be a factor in Fermi’s paradox because, as explained in note 1, below, biotechnology is likely to be an inevitable development in advanced civilizations.

To start, let’s be very generous with our hypothesized E and P by assuming that only 10 people in a civilization have access to civilization-ending biotechnology, and that each has only one chance in a million annually of pulling the trigger. Equation A3 in the paper predicts a median lifespan of 70,000 years in this situation, meaning that, given a large number of such civilizations, half would be expected to survive 70,000 years.

That’s the happiest number we’ve seen yet!

But median lifespan is not the whole story. The paper’s model happens to tell us that, no matter what the median lifespan is, after just 80 times that duration, only one civilization in 1,000,000,000,000,000,000,000,000 (that’s 24 zeroes again) will still be alive.

That is a remarkable result. It predicts that, if every star in the universe had a technical civilization like the example above, at the time our earliest ancestors were first starting to walk upright 5.6 million years ago, then only one civilization would have survived until now. Five million years is an eye-blink in the universe’s history, just 0.04% of its age. In other words, even if advanced civilizations are common in space, they may be rare in time.

The graph below shows the survival of civilizations for other E and P, assuming we start with a civilization in every star system. It plots the number of surviving civilizations over time for 29 different combinations of E and P. It turns out that this reduces to just 7 different survival curves, depending on the value of E multiplied by P. When the survival curve hits the x-axis, only one civilization is left. The rightmost curve hits the x-axis at 5.6 million years.

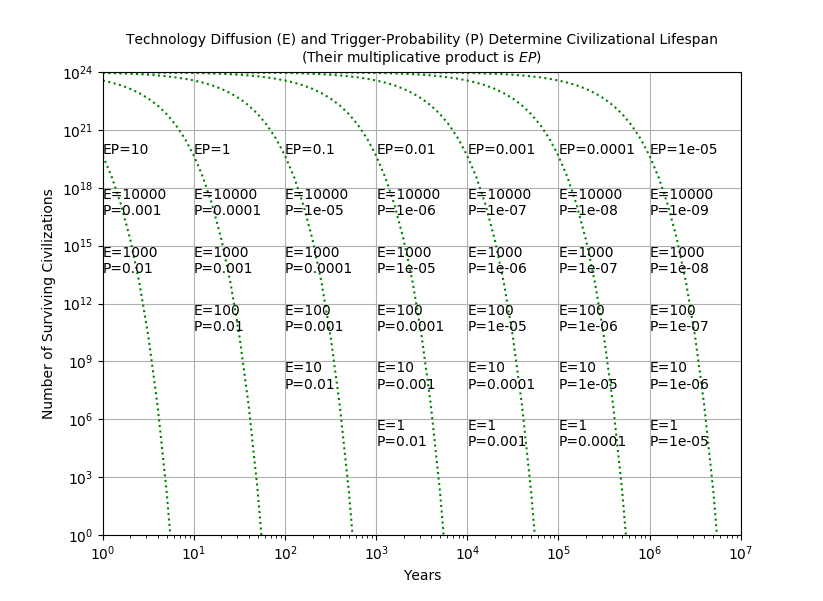It is hard to find in the graph any good news for the long-term survival of advanced civilizations in the universe. As a shorthand, if a civilization has a given E and P, a universe of such civilizations is empty in 56÷(E×P) years.

Still, it is important to make a few comments.

• The paper describes several assumptions behind its mathematical models. The longer the models are applied, the less likely the assumptions will hold. It is not clear, however, whether diverging from the assumptions will shorten or lessen the predicted lifespans. For example, figure 4 in the paper shows that a growth in E of just 1% per year can shorten civilizational lifespans even more.

• It may be hoped that colonization of other planets could outpace the rate of civilizational deaths. This is unlikely. Mathematically, the only way to outpace the model’s civilizational death rate is to colonize at an exponential rate (because the decline in civilization numbers is exponential). We can be reasonably sure that exponential colonization has not occurred in our galaxy because, if it had occurred over long periods of time, the galaxy would be filled-to-bursting with advanced civilizations, and we just don’t see that. A steady-state balance between exponential dying and exponential colonizing could occur, but it would be a delicate affair.

What Does It All Mean?

The paper shows that, once a civilization-ending technology exists, the continued survival of civilization is merely a numbers game. What to do?

That question has bedeviled the human race since the 1940s, when some of its members first realized we had the capacity to erase what millennia of progress have so painfully built. In all cases of existential threat, whether it is nuclear weapons, or asteroid impact, or climate change, or super-volcanism, or plagues, effective response must be built on a foundation of understanding. Continued exploration of such threats, with wide discussion to make them less abstract, is, therefore, the beginning. The emptiness of the universe suggests that successfully mitigating them is very hard … and that we better get to work.

---

Notes:

[1] Reasoning for the universality of biotechnology starts with the safe assumptions that all life forms are subject to disease and that all intelligent life will, as a result of evolution, have self-preservation drives at the individual or group level. This means that intelligence leads to a desire for medicines, and desire for medicines leads to technology that manipulates the fundamental genetic processes that define life, i.e. biotechnology. [Return to text]

The CA-ANG has an unofficial wiki at ANGSG.com. (It redirects to a wiki on Github.com.)

It functions more or less as a peripheral brain for State Air Surgeons, a place to put items that fall into any of several classes:

• Infrequently used material (example: forms for screening wildfire handcrews).

• Reminders to wing personnel about informal policies, and clarifications that are hard to find in regulations.

• Current and old regulations. (Sometimes old regulations are important in deciding the legality of past actions.)

In short, it’s a storehouse for useful things that don’t always rise to the level of memorization. If you have something you want stored, let me know. The site has storage limits, so a bit of editorial discretion is warranted.

The wiki is not updated frequently. In many places it is not current. So perhaps it is best viewed as a starting point for your queries.

If someone has a burning desire to transform it into a more useful site, let me know. Github is a platform for collaborative projects, so it should not be too tough to make a transition. I will, however, ask you to do the homework on how that would be done! :-)

To the Editor:

“The Popeye sign,” described in the Journal as a marked bulge in the upper arm after rupture of the biceps tendon (1), should more correctly have been called “a Popeye sign,” given that the term “Popeye arm” has also been applied to patients with fascio-scapulo-humeral muscular dystrophy who have wasting of the biceps combined with preserved deltoid and forearm musculature (2).

The confusion is understandable to anyone familiar with Popeye-the-Sailorman’s complex and dynamic upper limb anatomy. In his baseline state, Popeye exhibited the forearm muscular hypertrophy common among sailors of his era (the 1930s), for whom scraping paint was a frequent duty (3). To science’s detriment, the instantaneous biceps hypertrophy that Popeye experienced after oral spinach ingestion remains physiologically unexplained.

Thus, for maximal clarity, an eponymical purist would use the terms “pre-spinach Popeye sign” and “post-spinach Popeye sign,” respectively, in cases of fascio-scapulo-humeral muscular dystrophy and biceps tendon rupture.

If you’re the US Food and Drug Administration (FDA), you have a lot on your plate. But the train that is barreling right at you – the behemoth that is qualitatively different from everything you’ve encountered to date – is artificial intelligence in medicine.

How on earth are you going to regulate software that purports to be just as smart as a physician?

It’s much different from traditional FDA tasks like regulating an x-ray machine, which, after all, has only to record an image safely and accurately, and is something that engineers can by themselves confirm.

However, an A.I. “decision support” system for x-rays can fail in thousands of different ways when it tries to detect abnormalities or suggest diagnoses. The standard medical textbook for interpreting chest x-rays is 870 pages long – how can any software developer get all of that right? How can the FDA test all the possible failure modes?

The answer is: they can’t. Fortunately, they don’t have to. Instead, the linchpin of regulating medical A.I. systems can be two simple requirements: (1) every time a system provides a suggestion to a physician, the system asks the physician to rate the correctness or appropriateness of the suggestion, and (2) every rating is sent to the FDA, where it is tallied and made public on their web site.

In this way, A.I. systems are rated just as physicians assess each other: continuously, and in every interaction. This is obvious medical sociology. If Dr. Jones in some hospital starts to make squirrelly diagnoses or boneheaded readings, she will soon find her business drying up because her physician colleagues won’t trust her.

The same approach will work when “Dr. Jones” is an A.I. software package.

Thus, the FDA should set some minimum level of competence that allows reasonable A.I. products to get on the market, just as it does with the non-A.I. devices it regulates. After that, public ratings should be required, so that each product lives or dies by its performance in the marketplace, not by marketing budgets or slick advertisements.

As always, sunshine makes the best disinfectant, and it’s what you’d want in an A.I. system that was working on you.

Let’s examine some ramifications of this regulatory approach.

First, it ensures that manufacturers keep their system up to date. If a new disease like Zika virus comes along, which previously wasn’t in the A.I. system, the system will rapidly (and publicly) accumulate lots of errors. Manufacturers will therefore rush to update the system.

Second – similarly – it drives companies to widen their product’s coverage. An A.I. system that lacked moyamoya disease in its training may sail through pre-market testing on only a few hundred patients, but if applied to 200,000 patients across the world, systematic errors in moyamoya patients are more likely to become apparent and stimulate a new round of training that includes moyamoya disease.

Third, it fosters innovation. The FDA will be able to relax the minimum level of competence an A.I. product must demonstrate before being allowed on the market if it (the FDA) is assured that marketplace competition will perform the same functions as regulation. Make no mistake, American businesses will have many challengers in the medical A.I. world, and this factor will let our companies get to market faster.

Fourth, it will put physicians in the frame of mind to question the A.I. system’s advice at every turn. This is essential, because no manufacturer is ever going to claim its system replaces physician judgement. Instead, manufacturers will say their system provides information that a physician considers when making the official decision. Thus, always asking the physician to rate the A.I. advice will remind the physician that s/he is ultimately in control.

Fifth, this is a capability that every responsible software manufacturer should want to include in their systems. Responsible manufacturers want to fix bugs and shortcomings, and so they want to discover them. Manufacturers may even appreciate publicly-demonstrated imperfection, as it could enable them to defeat lawsuits arising from bad advice, by showing that the public had absolutely no reason to believe their system was perfect.

Of course, several specifics need addressing. What specific ratings questions should be posed to physicians? (They must be robust and quick.) How do we encourage physicians to change their ratings a month later, when the true diagnosis finally emerges? How do we prevent gaming of the ratings?

Ratings systems on the Internet are not only ubiquitous already, but have proven their value across many application areas. We are fortunate that such simple software can help us control the most complex software.

To the Editor:

West (*) describes angiogenesis, erythropoiesis, and vasoconstriction as clinical sequelae arising from chronically hypoxic tissues at altitude. Another, similar, effect is solid-organ hyperplasia.

In the late 1960s a Peruvian medical student observed several-fold enlargement of the carotid bodies in Andean altitude dwellers (1,2). The degree of enlargment increased with time spent at altitude and, in animal models, reversed after restoration of normoxia (3). Interestingly, this hyperplasia is mediated via endothelin signalling, not by hypoxia-inducible-factors (4).

Tissue hyperplasia may also occur in hypoxic patients at sea level. For example, even before the Peruvian discovery, hyperplasia – and sometimes malignancy – of adrenal chromaffin cells, i.e. pheochromocytomas, were described in adults having uncorrected cyanotic congenital heart disease (5). Carotid body cells and adrenal chromaffin cells have similar lineage (from the neural crest) and similar function (oxygen sensing).